Домашня самостійна робота №6

(Сторінка 174)

1. Яке з поданих чисел є дільником числа 24?

Відповідь: 6.

2. Яке з поданих чисел є кратним числу 9?

Відповідь: 27.

3. Яке з поданих чисел є простим числом?

Відповідь: 29.

4. Яку із запропонованих цифр можна поставити замість зірочки в запису числа 5*41, щоб воно стало кратним 3?

5 + 2 + 4 + 1 = 12 - це число кратне 3.
Відповідь: 2.

5. Знайди найбільший спільний дільник чисел 126 і 210.

126 = 2 ⋅ 3 ⋅ 3 ⋅ 7
210 = 2 ⋅ 3 ⋅ 5 ⋅ 7
НСД (126; 210) = 2 ⋅ 3 ⋅ 7 = 42.
Відповідь: 42.

6. Знайди найменше спільне кратне чисел 60 і 140.

60 = 2 ⋅ 2 ⋅ 3 ⋅ 5
140 = 2 ⋅ 2 ⋅ 5 ⋅ 7
НСК (60; 140) = 2 ⋅ 2 ⋅ 3 ⋅ 5 ⋅ 7 = 420
Відповідь: 420.

7. Із цифр 1, 5 і 9 утвори деяке трицифрове число так, щоб цифри в числі не повторювалися. Яке з тверджень буде правильним для цього числа?

Один з можливих варіантів такого числа – 159.
Тепер розглянемо кожне з тверджень:
Число 159 є непарним, оскільки остання цифра (9) є непарною.
Число 159 не є простим, оскільки воно має дільники (наприклад, 3 та 53).
Число 159 не є кратним 9, оскільки сума його цифр (1 + 5 + 9 = 15) не дорівнює 9.
Число 159 є кратним 3, оскільки сума його цифр (1 + 5 + 9 = 15) дорівнює 3, і тому воно ділиться націло на 3.
Відповідь: число є кратним 3.

8. Знайди частку від ділення числа 2 ⋅ 3 ⋅ 7 ⋅ 11 ⋅ 13 на число 3 ⋅ 7 ⋅ 13.

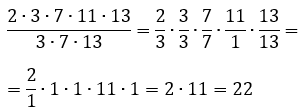
Відповідь: 22.

9. Укажи число, що є взаємно простим із числом 330.

330 = 2 ⋅ 3 ⋅ 5 ⋅ 11
91 = 7 ⋅ 13
Ці числа мають різні прості множники. Найбільший спільний дільник (НСД) між ними дорівнює 1, що означає, що вони взаємно прості.
Відповідь: 91.

10. Знайди найменше п’ятицифрове число, кратне числу 37.

10 000 - не є кратним 37.
10 001 - не є кратним 37.
10 002 - не є кратним 37.
10 027 - це число є кратним 37, оскільки 10 027 : 37 = 271.
Відповідь: 10 027.

11. У запису числа 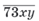постав замість х і у такі цифри, щоб утворене число було кратне числа 2, 5 і 9.

2 ⋅ 5 ⋅ 9 = 90
у = 0 тому, що числа які діляться на 90 закінчуються на 0
73х : 9
7 + 3 + х = 10 + х найближчий це 18 ⇒ 10 + х = 18
х = 18 – 10 = 8
Відповідь: х = 8, у = 0.

12. Між шкільними бібліотеками деякого регіону розподілили 190 словників з англійської мови й 114 словників з німецької мови. Скільки шкіл у цьому регіоні, якщо відомо, що їх більше за 20 і кожна школа отримала однакову кількість словників кожного виду?

190 = 1 ⋅ 114 + 76
114 = 1 ⋅ 76 + 38
НСД (190; 114) = 38
Кількість шкіл = (190 + 114) : 38 = 304 : 38 = 8
Відповідь: 38.