Діагностична (контрольна) робота ДР-6 Варіант 4
(Сторінка 59)
- Укажи дільник числа 18.
А. 144
Б. 6✅
В. 5
Г. 4
-
Укажи число, що є кратним числу 2.
А. 167
Б. 165
В. 168✅
Г. 163
- Розклади на прості множники число 18.
А. 2 · 2 · 3
Б. 2 · 2 · 2
В. 3 · 3 · 3
Г. 2 · 3 · 3✅
- Укажи пару чисел, у якій обидва числа є складеними.
А. 14 і 15✅
Б. 7 і 18
В. 5 і 17
Г. 16 і 3
- Знайди найбільший спільний дільник чисел 234 і 65.
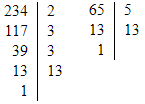
234 = 2 · 3 · 3 · 13
65 = 5 · 13
НСД (234; 65) = 13
Відповідь: 13.
- Знайди найменше спільне кратне чисел 35 і 40.
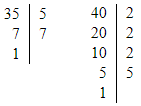
35 = 5 · 7
40 = 2 · 2 · 2 · 5
НСК (35; 40) = 2 · 2 · 2 · 5 · 7 = 280
Відповідь: 280.
- Чи є числа 165 і 308 взаємно простими?
Числа називаються взаємно простими, якщо їх найбільший спільний дільник дорівнює 1.
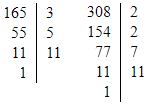
165 = 3 · 5 · 11
308 = 2 · 2 · 7 · 11
НСД (165; 308) = 11 ≠ 1
Відповідь: ні.
-
Якою цифрою треба замінити «зірочку» в числі 3203*, щоб отримане число було кратним числу: 1) 5; 2) 3? Знайди всі розв'язки.
1) Число ділиться на 5, якщо воно закінчується на 5 або 0: 32 035, 32 030.
2) Число ділиться на 3, якщо сума всіх його цифр ділиться на 3 (3 + 2 + 0 + 3 + * = 8 + *): 32 031, 32 034, 32 037.
-
Туристи для сплаву по річці можуть розміститися у 15-місних або 9-місних човнах. В обох випадках вільних місць не залишиться. Скільки всього туристів, якщо їх більше за 87, але менше ніж 129?
Кількість туристів має ділитися на 15 і на 9. Знайдемо найменше спільне кратне цих чисел:
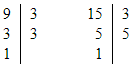
9 = 3 · 3
15 = 3 · 5
НСК (9; 15) = 3 · 3 · 5 = 45
Це мінімальна кількість туристів, які можуть розміститися порівну і в 9-місних і в 15-місних човнах, але в умові сказано, що їх кількість має знаходитись в інтервалі між 87 і 129. Тому напишемо декілька перших значень кратних числу 45:
45 · 2 = 90 (87 < 90 < 129)
45 · 3 = 135 > 129
Заданому інтервалу відповідає число 90.
Відповідь: всього 90 туристів.
